There was a problem asked on the first version of the Mega Test, something like “What is the maximum number of discrete spaces one can create from three interpenetrating cubes.” I tried to visualise this one for a month, and even had a go at trying to make one out of toothpicks, but gave up and guessed. I am 99% sure I got it wrong, but I don’t remember what I answered.
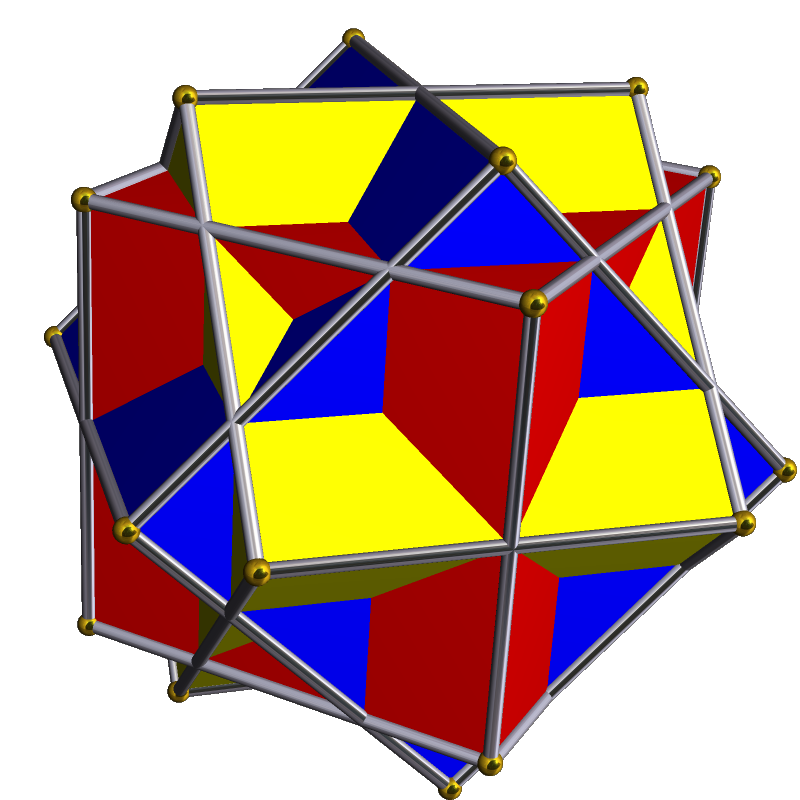
By The original uploader was Tomruen at English Wikipedia. – Transferred from en.wikipedia to Commons., CC BY-SA 3.0, Link
I learned about a year ago that the figure has been used in some discussion by a mathematician named John Skilling. I keep looking at it and thinking I get it, then it slips away. Unsurprisingly, MC Escher used it in a drawing, because of course he did. It is the most notoriously difficult problem on the Mega Test, which used to be used by the ultra-high IQ societies to sort amongst the highest scorers. I used to correspond with test designer Ron Hoeflin, who describes himself as a Schizoid Personality Disorder, and I believe it. Even among the highest scorers on the Mega, those who got over 45 out of 48 or better, less than a third got this one right. As I had already taken the test years ago and am not allowed a retake, I didn’t think it would be cheating to scour the web to see if I could suss out the answer. The most common answer is 72 discrete spaces, which seems logical: 24 corners each intercepted by two planes, 24 x 3 = 72. Apparently that is wrong. The answer is greater than 68, however, because some determined SOB built one of these suckers out of rods and colored cellophane and then counted and got to 68 definite and answered that. He wondered if he might have missed at least one. Apparently even when you’ve got a hard model it’s had to keep track. He concluded he got it wrong from his returned grade and the subsequent discussion by email among people who had qualified for the highest society. He now thinks the answer must be 69. Ron’s not telling. One of the very few people who have gotten a 47 or the person who got a 48 must also know.
The parallel question on the other side of the test is 5 interpenetrating spheres. On both problems I fooled around with the idea of solids of differing sizes, but concluded there was no advantage in creating discrete spaces that way.
This was part of my eventually learning that I am not exceptional in my spatial intelligence, though it took me a long time to learn and admit that. You can have a go at the answer, but I can’t confirm if you got it right or not. For myself, I would like an explanation why 72 is not right, because that makes the most sense to me.
120 is my guess (and probably wrong). 40 per cube x 3 cubes. I couldn’t have even begun to figure this out without the picture.
By discrete space, do you mean an enclosed cavity consisting of strips of one and only one cube face? If so, then I count less than 68.
If the cavity can be enclosed by strips of two overlapping cube faces, somewhat like a Boolean union, then I think it’s probably around 68. There would be a lot going on under the hood, so to speak.
I should add that I’m not doing any whizbang math calculations or anything like that. I just recreated this shape in a 3D modeler probably similar to that Wikipedia image, then cut away all the cavities.
@ Grurray – yes, the latter. In the 1980s were there 3D modelers on computers?
Hmmm, I had to look that up. There were CAD programs like Autodesk that started using 3D at that time, but those would’ve been industrial applications on UNIX platforms. There were also the 3D graphics and animation programs just emerging back then, but that stuff would’ve been captive possessions of movie production companies. I can’t think of anything available to a hobbyist on a PC.
I followed the links from the image and found the free downloadable program that was used for this shape. Maybe someone else wants to take a crack at it
https://www.software3d.com/Stella.php
Yes, by the mid-late 1980s you could have modeled it in 3d on AutoCAD. I took a job doing CAD work for fill-in in 1989, and even then it was “AutoCAD 10”, which was actually about 5 or 6 in terms of “real, commercial” versions.
I’m thinking it’ll be more than 72, because there’s going to be more than one likely entirely internal space, too. But that’s just visualizing it quickly. Just feels like there will be some unexpected intersections, there, not involving the vertexes. Maybe not. :-/
P.S., by the mid 1990s, you could posdef do 3D in AutoCAD (in addition to 3DStudio, which was more for rendering semi-photo/video grade imagery and animations)… I did a building in full 3d for a massing study on an addition to an existing “historic” space to make it also match up with ADA reqs while still retaining the original structure as much as possible. I also did the final in 3D just because we had it already mostly there. It helped spot an unusual problem with regards to stairs+entrances+handicap ramps+very-very-steep-roofs — the constraints had the roof rafters penetrating the expected ceiling height, said height constrained by the obvious floor requirements, but the exterior wall height constrained by the existing structure and its own roof height. At one corner of the building, the rafter came down into the open stairway access. Spotting that saved a good bit in post-bid/during construction plan modification costs…
Those were the good old days when 3D was just taking off. Back before the the Eternal September. There was the genuine feeling that the proverbial third eye was opening up.
It did improve so many things. Speed, safety, efficiency went off the charts. However, we lost something too. Regarding the 3D compound cube shape, I have the 3D model and still can’t figure it out. How amazing it must be for someone to determine it out without digital help.
How enriching it was to design and build structures with only tried and true rules, tribal knowledge, and traditions. We didn’t have the spiraling, ribboning, modern art-level buildings we have now, but we did have something closer to earth that kept us all more together and cohesive.